【Unity】シェーダで穴をあけるマッピング

昨日

本記事は Unity Advent Calendar 2022 の 19日目の記事です。
前日の記事はwakapippiさんの「【Unity】音声データからピッチ推定を行う」でした！
qiita.com

AudioSource.GetSpectrumDataで簡単にできるのかなと思っていましたが、負荷や精度に問題があるとは知らず、とても勉強になりました。
マイクからの入力だけではなく、ゲームキャラクターの口パクにも利用できそうですね！

はじめに

本記事では、Unityにてシェーダで穴をあける実装の解説になります。
興味深い記事を見つけてはブラウザのタグに保管されていたので、この機会にUnityで実装しつつ日本語訳してみました。
視差オクルージョンマッピングのように見えますが、円形の穴に特化したものになります。

参考

こちらがその興味深い記事です。
大変わかりやすく丁寧なので是非ご覧ください（添付画像も引用させていただいております）
medium.com

（動画の見せ方もカッコイイ）

完成図

解説向けに必要最低限の実装になっています。

完成品もあるので興味のある方はご覧ください
github.com

仕組み

穴は「視点/視線」によって変化します。

今回は視線とピクセルのワールド座標を用いて、穴との衝突位置を計算します。

Procedurally generated hole in Blender3D（@Hans Chiuさん）から引用

実装

準備

次のようなシェーダを準備します。

Shader "Custom/HoleShader" 
{
    Properties
    {
        _MainTex ("Texture", 2D) = "white" {}
        _HoleRadius ("Hole Radius", Float) = 1.0
        _HolePosition ("Hole Position", Vector) = (0.0, 0.0, 0.0, 0.0)
    }

    SubShader
    {
        Tags
        {
            "RenderType"="Opaque"
        }

        Pass
        {
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"

            struct Attributes
            {
                float4 positionOS : POSITION;
                float2 uv : TEXCOORD0;
                float3 normal : NORMAL;
            };

            struct Varyings
            {
                float4 positionCS : SV_POSITION;
                float2 uv : TEXCOORD0;
                float3 normal : NORMAL;
                float3 positionWS : TEXCOORD1;
            };

            sampler2D _MainTex;
            float _HoleRadius;
            float3 _HolePosition;

            Varyings vert (Attributes v)
            {
                Varyings o;
                o.positionCS = UnityObjectToClipPos(v.positionOS);
                o.positionWS = mul(unity_ObjectToWorld, v.positionOS);
                o.normal = UnityObjectToWorldNormal(v.normal);
                o.uv = v.uv;
                return o;
            }

            float4 frag (Varyings i) : SV_Target
            {
                return float4(1.0, 1.0, 1.0, 1.0);
            }
            ENDCG
      }
}

このシェーダに実装していきます（主にピクセルシェーダ）。
ピクセルシェーダに渡すべき情報は概ね用意してありますので、それら入力する変数を説明します。

変数名	内容
Varyings::positionCS	ピクセルのクリッピング座標（穴の計算には利用しません）
Varyings::positionWS	ピクセルのワールド座標
Varyings::normal	法線
Varyings::uv	テクスチャUV
_MainTex	テクスチャ
_HoleRadius	穴の半径
_HolePosition	穴のワールド座標。解説では原点（0, 0, 0）です。

マテリアルを作成し、このシェーダを割り当てたものをPlaneに適応します。
Planeの座標は原点かつ回転していない状態です。

円との衝突地点を求める

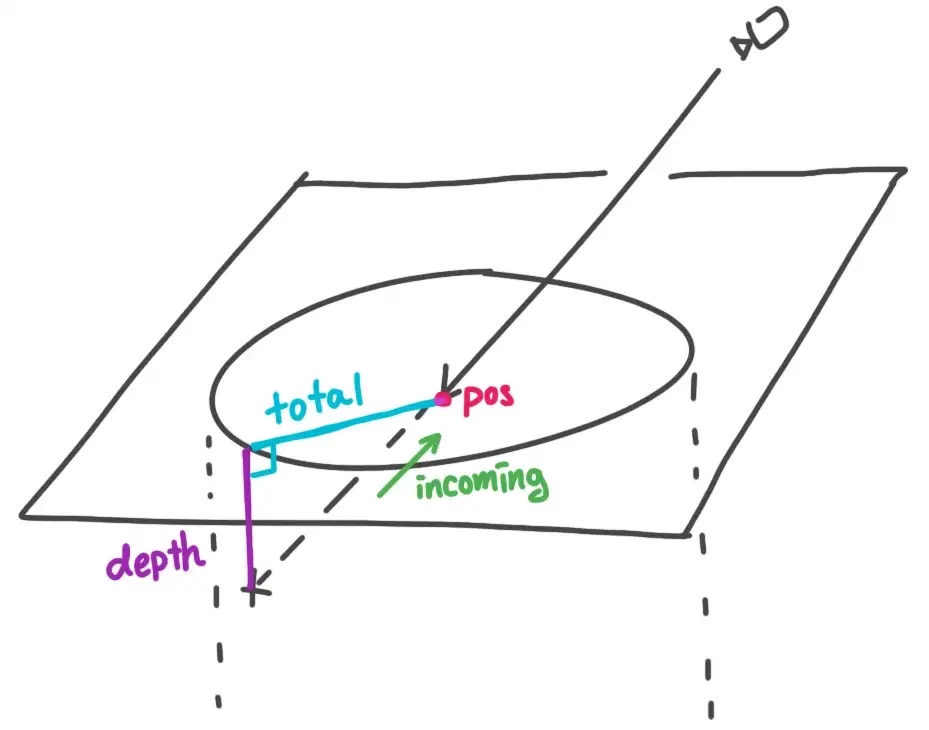
下の図のように、４つの変数を利用し、平面上の円との衝突位置を求めます。

変数名	内容
origin	穴の中心座標（=_HolePosition）
radius	穴の半径（=_HoleRadius）
incoming（以降、incomingDir）	ピクセルからカメラに向かう方向ベクトル
position（以降、positionDir）	穴の中心からピクセルのワールド座標に向かう方向ベクトル

float4 frag (Varyings i) : SV_Target
{
    // 変数の準備
    float3 cameraPos = _WorldSpaceCameraPos;
    float3 cameraDir = normalize(i.positionWS - cameraPos);

    float3 origin = _HolePosition;
    float3 positionDir = i.positionWS - origin;
    float3 position2DDir = positionDir * float3(1,0,1);
    float3 incomingDir = -cameraDir;
    float3 incoming2DDir = normalize(incomingDir * float3(1,0,1));

    return float4(1.0, 1.0, 1.0, 1.0);
}

これら４つの情報を利用し、下の図のように「Total」（以降TotalLength）を計算します。
こちらはY軸成分を削除した２Ｄ平面で計算します（ご注意）。なのでTotalLengthは平面上の線分の長さになります。

このTotalLengthは２つの三角形から長さを求めます。
１つ目は下の図の三角形です。TotalLengthが内包する長さは、positionDirとincomingDirの内積になります。

２つ目は下の図の三角形です。ピタゴラスの定理を使って x を求めます。y は上の画像にあったように、positionDirとincomingDirの外積で得られたベクトルの長さになります。
$\begin{align} \boldsymbol{radius}^2 &= \boldsymbol{x}^2 + \boldsymbol{y}^2 \\ \boldsymbol{x} &= \sqrt{\boldsymbol{radius}^2 - \boldsymbol{y}^2} \\ \boldsymbol{x} &= \sqrt{\boldsymbol{radius}^2 - | \boldsymbol{positionDir} \times \boldsymbol{incomingDir}|^2} \end{align}$

TotalLengthはこれら２つの三角形の１辺を足し合わせることで計算できます。
$\begin{align} \boldsymbol{totalLength} &= \boldsymbol{positionDir} \cdot \boldsymbol{incomingDir} + \sqrt{\boldsymbol{radius}^2 - | \boldsymbol{positionDir} \times \boldsymbol{incomingDir}|^2} \end{align}$

float4 frag (Varyings i) : SV_Target
{
    // 変数の準備
    …

    // TotalLength = positionDir・incomingDir + sqrt(radius^2 - |position×incoming|^2);
    float3 crossPosIncom = cross(position2DDir, incoming2DDir);
    float dotPosIncom = dot(position2DDir, incoming2DDir);
    float totalLength = dotPosIncom + sqrt(pow(_HoleRadius, 2.0) - pow(length(crossPosIncom), 2.0));

    return float4(1.0, 1.0, 1.0, 1.0)  * saturate(totalLength);
}

うっすら穴のようなものが見えるようになります。

深さを求める

２Ｄ平面状の円との距離が計算できたので、続いて衝突する深さ（Depth）を計算します。

深さは下の図のような２つの三角形を考えます。
２つの三角形の斜辺は、共通してincomingDirのものです。totalとxは平面上にある線分なので、２つの三角形は相似の関係にあります。相似ということは３辺の比率が同じということなので、比例式を使ってDepthを求めることができます。

IncomingのZに関しまして、参考記事のBlenderはZ upなので、UnityのY upに置き換えて考えます。

$\begin{align} \boldsymbol{depth} : \boldsymbol{totalLength} &= \boldsymbol{Y} : \boldsymbol{X} \\ \boldsymbol{depth} \times \boldsymbol{X} &= \boldsymbol{totalLength} \times \boldsymbol{Y} \\ \boldsymbol{depth} &= \frac{\boldsymbol{totalLength} \times \boldsymbol{Y}}{\boldsymbol{X}} \\ \end{align}$

IncomingのXは、これまたピタゴラスの定理で長さを求めます。IncomingDirは単位ベクトルなので大きさは１となりますので、次の式で求めることができます。

$\begin{align} \boldsymbol{1}^2 &= \boldsymbol{X}^2 + \boldsymbol{Y} \\ \boldsymbol{X} &= \sqrt{\boldsymbol{1}^2 - \boldsymbol{Y}^2} \end{align}$

float4 frag (Varyings i) : SV_Target
{
    // 変数の準備
    …

    // TotalLength = positionDir・incomingDir + sqrt(radius^2 - |position×incoming|^2);
    …

    // Depth = TotalLength * incomingY / incomingX
    float incomingX = sqrt(1.0 - pow(incomingDir.y, 2.0));
    float depth = totalLength * incomingDir.y / incomingX;

    return float4(1.0, 1.0, 1.0, 1.0)  * frac(depth);
}

穴の形に沿って、縞模様が見えるようになります。

穴の衝突位置を求める

Depthの計算ができたので、穴の衝突位置を求めることができます。直行するDepthとTotalLengthの２辺の間の斜辺がincomingDirの長さにあたるので、これをincomingDirに乗算するだけです。ただし、incomingDirはワールド座標からカメラに向かうベクトルなので、カメラからワールド座標に向かうcameraDirを利用します。

float4 frag (Varyings i) : SV_Target
{
    …

    float3 position = i.positionWS + cameraDir * length(float3(totalLength, depth, 0.0));

    …
}

ライティング

穴の衝突地点から光源の方向に地表まで進むことによって、進んだ地点に穴があるかどうかで影になるかを判断します。

こちらも深さを求めるときと同様に、比例式を使ってOffsetを計算します。

float4 frag (Varyings i) : SV_Target
{
    // 変数の準備
    …

    // TotalLength = positionDir・incomingDir + sqrt(radius^2 - |position×incoming|^2);
    …

    // Depth = TotalLength * incomingY / incomingX
    …

    // Lighting
    float3 lightDir = _WorldSpaceLightPos0.xyz;
    float lightDirX = sqrt(1.0 - pow(lightDir.y, 2.0));
    float offset = depth * lightDirX / abs(lightDir.y);
    float2 positionToLight = position.xz + lightDir.xz * offset;
    float holeAtten = step(distance(_HolePosition.xz, positionToLight), _HoleRadius) * 0.5 + 0.5;

    return float4(1.0, 1.0, 1.0, 1.0)  * frac(holeAtten);
}

positionToLight が穴の衝突地点から光源方向に地表まで進んだ座標です。この座標と穴の中心座標（_HolePosition）の距離を計算し、穴の半径（_HoleRadius）と比較します。穴の半径より小さかったら穴の中なので光が当たる箇所となり、穴の半径より大きかったら穴の外なので影となります。

パキッとした影なので、もう少しソフトにします。

float4 frag (Varyings i) : SV_Target
{
    …

    float holeAtten = smoothstep(-0.5, 0.5, _HoleRadius - distance(_HolePosition.xz, positionToLight)) * 0.5 + 0.5;

    …
}

せっかくなのでハーフランバートも追加します。
穴に衝突した地点の法線は、穴の中心に向かうベクトル（Y軸を無視した２Ｄ空間上）になります。

float4 frag (Varyings i) : SV_Target
{
    …

    // Lighting
    …

    // Half-Lambert
    float3 holeNormal = normalize(_HolePosition - float3(position.x, _HolePosition.y, position.z));
    holeAtten = min(holeAtten, max(pow(dot(_WorldSpaceLightPos0.xyz, holeNormal) * 0.5 + 0.5, 2.0), 0.25));

    …
}

マスクする

穴が透けて見えているので、今までの計算は穴の箇所だけになるようにマスクします。ピクセルのワールド座標（Varyings::positionWS）と穴の中心座標（_HolePosition）の距離を計算し、穴の半径より小さい箇所だけマスクします。

float4 frag (Varyings i) : SV_Target
{
    …

    // Mask
    float mask = step(distance(i.positionWS, _HolePosition), _HoleRadius);

    // Half-Lambert
    float planeAtten = max(pow(dot(_WorldSpaceLightPos0.xyz, i.normal) * 0.5 + 0.5, 2.0), 0.25); // 平面の陰影を追加
    …
    
    return float4(1,1,1,1) * lerp(planeAtten, holeAtten, mask); // マスクする
}

穴が見えるようになりました。

黒くフェードアウトする

穴の深い位置になるほど光は届かなくなるので、深くなるにつれ真っ暗になります。正確な計算はしませんが、Depthに合わせて黒フェードする実装をします。まずPropertiesに黒フェード用の入力変数を追加します。

Properties
{
    …

    [PowerSlider(10.0)] _HoleBlackFade ("Hole BlackFade", Range(0.1, 1.0)) = 0.18
    _HoleBlackFadeDepth ("Hole BlackFade Depth", Range(0.0, 10.0)) = 2.0
}

変数名	内容
_HoleBlackFade	黒フェードするグラデーションの深さ
_HoleBlackFadeDepth	黒フェードを開始する位置（深さ）

float _HoleBlackFade;
float _HoleBlackFadeDepth;

float4 frag (Varyings i) : SV_Target
{
    …

    // Mask
　…

    // Half-Lambert
    …
    holeAtten = min(holeAtten, max(pow(dot(_WorldSpaceLightPos0.xyz, holeNormal) * 0.5 + 0.5, 2.0), 0.25));
    holeAtten *= saturate(_HoleBlackFadeDepth - pow(depth, _HoleBlackFade)); // 追加
    …
}

テクスチャを貼る

最後にテクスチャを貼ります。地表はVaryings::uvをそのまま利用して問題ありませんが、穴の中はマッピングする必要があります。
穴の中のマッピングは、穴の中心から衝突地点の角度をＵ軸、深さをV軸としてマッピングしてみました。

float4 frag (Varyings i) : SV_Target
{
    …

    // Depth = TotalLength * incomingY / incomingX
    …

    // TextureMapping Ground
    float4 col = tex2D(_MainTex, i.uv);

    // TextureMapping Hole
    float2 positionDiff = position.xz - _HolePosition.xz;
    float2 holeUV = float2(
        -(atan2(positionDiff.y, positionDiff.x) + UNITY_PI) / (2.0 * UNITY_PI), // U軸
        frac(-depth / (2.0 * UNITY_PI * _HoleRadius)));                         // V軸
    float4 holeCol = tex2D(_MainTex, holeUV);
    
    // Mask
    …
    col.rgb = lerp(col, holeCol, mask);

    // Half-Lambert
    …
    col.rgb *= lerp(planeAtten, holeAtten, mask);
    return col;
}

positionDiff は穴の中心座標から穴の衝突座標への方向ベクトルです。atan2関数を利用することで角度を計算します。atan2は-π～πの値が返るので、0.0～1.0になるように加工しＵ軸にしています。Ｖ軸はDepthを利用しますが、穴の円周の長さと一致するように加工しています。

おまけ

Varying::positionWSをタイリングすることで穴を増やしてみます。

float4 frag (Varyings i, out float outDepth : SV_Depth) : SV_Target
{
    float3 tiledPositionWS = i.positionWS;
    tiledPositionWS.xz = frac(i.positionWS.xz) * 10.0 - 5.0; // -5.0～5.0に加工

    …
     float3 positionDir = tiledPositionWS - origin;
    …

    // TotalLength = positionDir・incomingDir + sqrt(radius^2 - |position×incoming|^2);
    …

    // Depth = TotalLength * incomingY / incomingX
    …
    float3 position = tiledPositionWS + cameraDir * length(float3(totalLength, depth, 0.0));

    // TextureMapping Ground
    …

    // TextureMapping Hole
    …

    // Mask
    …
    float mask = step(distance(tiledPositionWS, _HolePosition), _HoleRadius);

    …
}