インテリアマッピング(interior mapping)~平面距離編~
はじめに
本記事は Unity Advent Calendar 2018 の 11日目 の記事です。
前日の記事は もんりぃ先生さん の「ごっこランドを支える技術 〜ビルド編〜」でした!
qiita.com
本記事では、インテリアマッピングの実装について簡単にまとめてみました。
最近発売されたPS4の「Marvel's Spider-Man」でちょっと話題になっていたので、
気になって調べてみました。本記事はその備忘録のようなものになります。
目次
インテリアマッピング(Interior Mapping)
インテリアマッピングとは、その名の通りビル等の建築物の室内装飾表現に用いられる描画表現です。前述にもありますが「Marvel's Spider-Man」や「Watch Dogs」等のゲームで使用されているみたいです。
The architecture in Spider-Man is some M.C. Escher shit.https://t.co/AKhtZUdtvQ pic.twitter.com/yvKSfowiHV
— chris person (@Papapishu) 2018年9月8日
お恥ずかしながら話題になるまで存在自体知りませんでした。
視線によって変わるので難しいのかなぁと思いきや、調べてみたら実装はとてもシンプルでした。

完成図
実装
無限平面
インテリアマッピングでは前述の通り「視点/視線」によって変化します。

視線の先は必ず壁、床、天井、オブジェクト(人、植木等)のいずれかの面に向けられますが、どの面が手前に描画されるのかは、それぞれの”距離”を求めることにより分かります。つまり視線と各面の交点を求め、手前にある面の色を描画することで奥行きが表現されます。

無限平面までの距離計算
ではどのようにして距離を求めるかというと、ベクトルの内積を使います。
内積と言えば下記のような特性があります。
・2つのベクトルが同じ向きなら、1を返す
・2つのベクトルが直角なら、0を返す
・2つのベクトルが逆の向きなら、-1を返す
ここでは距離を求めるのに「直行するベクトルの内積=0」という数式を利用します。

上の画像では、平面上にあるP0とP、平面の法線のベクトルがあります。
この2つのベクトルは必ず直角になる為、内積は必ず0になります。
P0とPは平面上であれば、どこにあっても同じ結果となります。

ここで視点のL0、視線のLを使ってPの位置となる式を考えます。
Pは平面上ならどこでも良いので、視線Lの長さをtとすれば、
「L0 + L * t = P」という式でPが求められそうです。
上記のことから、距離tを求めるには…

このように展開できます。つまり…?
P0 … 平面上の点(どこでもOK)
L0 … 視点
L … 視線ベクトル
n … 平面の法線
この情報が分かれば、視点から視線の先にある平面の"距離"が求められます。
シェーダに次のような関数を用意します。
// 線分と無限平面の衝突位置算出 // rayPos : レイの開始地点 // rayDir : レイの向き // planePos : 平面の座標 // planeNormal : 平面の法線 float GetIntersectLength(float3 rayPos, float3 rayDir, float3 planePos, float3 planeNormal) { return dot(planePos - rayPos, planeNormal) / dot(rayDir, planeNormal); }
これで無限平面を描画する準備が整いました!
え?っと思われるかと思いますが、インテリアマッピングの肝となる計算はこれだけなんです。
では早速、床となる平面を描画しましょう。
Shader "Custom/InteriorMappingTest" { Properties { _MainTex("Main Texture", 2D) = "white" } CGINCLUDE #include "UnityCG.cginc" #define INTERSECT_INF 999 sampler2D _MainTex; struct v2f { float4 pos : SV_POSITION; float3 objectViewDir : TEXCOORD0; float3 objectPos : TEXCOORD1; }; //--------------------------------------------------- // 線分と無限平面の衝突位置算出 // http://www.scratchapixel.com/lessons/3d-basic-rendering/minimal-ray-tracer-rendering-simple-shapes/ray-plane-and-ray-disk-intersection // rayPos : レイの開始地点 // rayDir : レイの向き // planePos : 平面の座標 // planeNormal : 平面の法線 float GetIntersectLength(float3 rayPos, float3 rayDir, float3 planePos, float3 planeNormal) { // 処理効率悪いので使用する側でカバー //if (dot(rayDir, planeNormal) <= 0) // return INTERSECT_INF; // (p - p0) ・n = 0 // (L0 + L*t - p0)・n = 0 // L*t・n + (L0 - p0)・n = 0 // (L0 - p0)・n = - L*t・n // ((L0 - p0)・n) / (L・n) = -t // ((p0 - L0)・n) / (L・n) = t return dot(planePos - rayPos, planeNormal) / dot(rayDir, planeNormal); } //--------------------------------------------------- v2f vert(appdata_base i) { v2f o; o.pos = UnityObjectToClipPos(i.vertex); // カメラから頂点位置への方向を求める(オブジェクト空間) o.objectViewDir = -ObjSpaceViewDir(i.vertex); o.objectPos = i.vertex; return o; } half4 frag(v2f i) : SV_TARGET { float3 rayDir = normalize(i.objectViewDir); float3 rayPos = i.objectPos; float3 planePos = float3(0, 0, 0); float3 planeNormal = float3(0, 0, 0); float intersect = INTERSECT_INF; float3 color = float3(0,0,0); // 床 { planeNormal = float3(0, 1, 0); planePos.xyz = 0.0; float i = GetIntersectLength(rayPos, rayDir, planePos, planeNormal); if (i < intersect) { intersect = i; color = float3(1.0, 1.0, 1.0); } } return half4(color, 1); } ENDCG SubShader { Tags { "RenderType"="Opaque" } Pass { CGPROGRAM #pragma target 2.0 #pragma vertex vert #pragma fragment frag ENDCG } } }
これで中心を境に床が描画されます。
しかし、これだけでは真っ白に描画されるだけになります。
何故なら1つの面の距離を求めても、平面が無限に続くので単色で埋め尽くされてしまうからです。

無限平面を交差
そこで上記の関数を使って壁を作ります。
やりかたは全く同じです。最終的に距離が一番短い(一番視点に近い)面の色を出力します。
// 左の壁 { planeNormal = float3(1, 0, 0); planePos.xyz = 0.0; float i = GetIntersectLength(rayPos, rayDir, planePos, planeNormal); if (i < intersect) { intersect = i; color = float3(0.8, 1.0, 0.8); } } // 奥の壁 { planeNormal = float3(0, 0, 1); planePos.xyz = 0.0; float i = GetIntersectLength(rayPos, rayDir, planePos, planeNormal); if (i < intersect) { intersect = i; color = float3(0.5, 0.8, 1.0); } }
ここでやっとそれらしい描画になります。
インテリアっぽくなるまで、あともうちょっとです!

無限平面の表裏
先程描画した平面の裏側も描画します。
無限平面の交差の際にやったように続々と追加しても構いませんが、視線に対して視認できる平面は必ず3つになります。例えば、床が見える視線の先に天井は映りえませんし、奥の壁が見える視線の先に壁の背面は映りえません。
これは平面の法線と視線との内積で判別することができます。
const float3 UpVec = float3(0, 1, 0); const float3 RightVec = float3(1, 0, 0); const float3 FrontVec = float3(0, 0, 1); // 床と天井 { float which = step(0.0, dot(rayDir, UpVec)); planeNormal = float3(0, lerp(1, -1, which), 0); planePos.xyz = 0.0; planePos.y -= lerp(0.5, -0.5, which); float i = GetIntersectLength(rayPos, rayDir, planePos, planeNormal); if (i < intersect) { intersect = i; color = float3(1.0, 1.0, 1.0); } } // 左右の壁 { float which = step(0.0, dot(rayDir, RightVec)); planeNormal = float3(lerp(1, -1, which), 0, 0); planePos.xyz = 0.0; planePos.x -= lerp(0.5, -0.5, which); float i = GetIntersectLength(rayPos, rayDir, planePos, planeNormal); if (i < intersect) { intersect = i; color = float3(0.8, 1.0, 0.8); } } // 奥の壁 { float which = step(0.0, dot(rayDir, FrontVec)); planeNormal = float3(0, 0, lerp(1, -1, which)); planePos.xyz = 0.0; planePos.z -= lerp(0.5, -0.5, which); float i = GetIntersectLength(rayPos, rayDir, planePos, planeNormal); if (i < intersect) { intersect = i; color = float3(0.5, 0.8, 1.0); } }
変数whichに対し、平面法線と視線が同じ向きなら1.0、逆向きなら0.0が代入されます。
そのwhichを元に、planeNormalの向きを変更しつつ、planePosも変えています。
Boxにマテリアルをアタッチすると綺麗に内側が表示されるようになったかと思います。
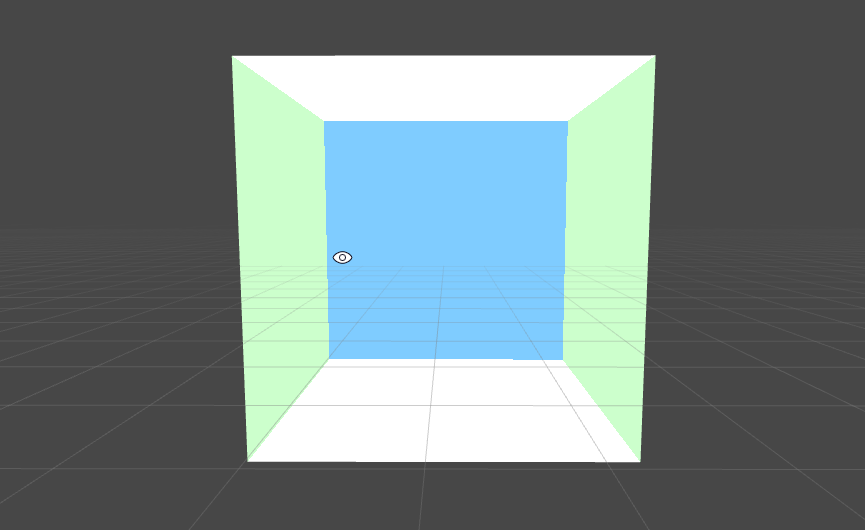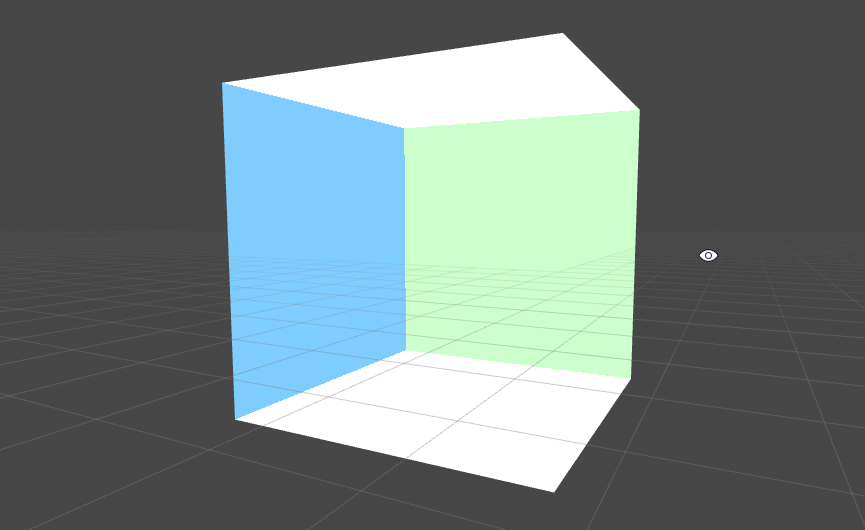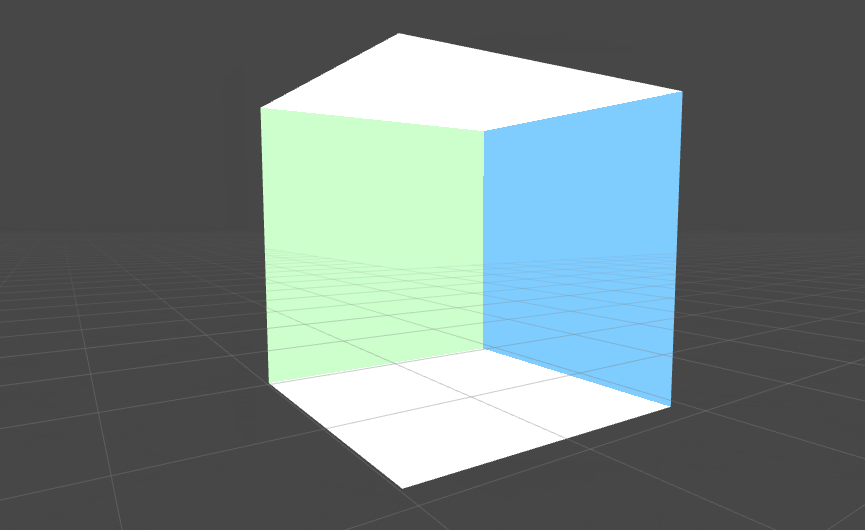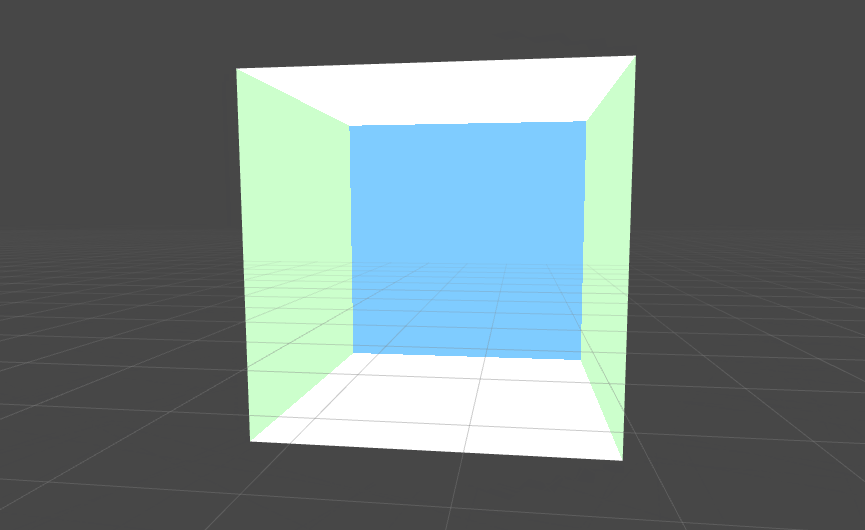
階層
インテリアマップの一番の魅力は、大量の部屋の内装を描画できるところにあります!
ビル等の部屋をモデリングで1部屋ずつ作りこむのは相当時間がかかりますし描画コストも上がります。しかしこのインテリアマップを用いれば、ビルのどの部屋も内装がしっかり作られているように見えますし、それでいて描画コストもそこそこ抑えられています。モバイルは厳しいですが、それ以外でしたらお手軽クオリティアップです!
では早速やっていきます。この実装もシンプルで、
視点に合わせてplanePosの位置を変えるだけです。イメージで言うと小数点を切り捨てるだけです。
float3 rayDir = normalize(i.objectViewDir); float3 rayPos = i.objectPos + rayDir * 0.0001; // 微妙に内側に入れることでZファイティングを防ぐ // 床と天井 { ... planePos.xyz = 0.0; planePos.y = ceil(rayPos.y); planePos.y -= lerp(1.0, 0.0, which); ... } // 左右の壁 { ... planePos.xyz = 0.0; planePos.x = ceil(rayPos.x); planePos.x -= lerp(1.0, 0.0, which); ... } // 奥の壁 { ... planePos.xyz = 0.0; planePos.z = ceil(rayPos.z); planePos.z -= lerp(1.0, 0.0, which); ... }
planePosの座標をrayPosの小数点切り捨て(ceil)で1Unit間隔で平面が表示されるようになりました。
さりげなくrayPosの初期化処理を修正しましたが、微妙に重要な処理になります。
今回この階層処理で1Unit間隔に綺麗にそろったことにより、さっきのrayPosと同じ座標に無限平面が位置してしまいました。それにより出力される平面の奥行き感が乱れてしまったので、若干(0.0001分)rayPosを前進させています。
折角なので、この間隔をInspectorで調整出来るようにしてみましょう。
Properties
{
...
_DistanceBetweenFloors ("Distance Between Floors", Float) = 0.25
_DistanceBetweenWalls ("Distance Between Walls", Float) = 0.25
}
float _DistanceBetweenFloors;
float _DistanceBetweenWalls;
half4 frag(v2f i) : SV_TARGET
{
...
// 床と天井
{
...
planePos.xyz = 0.0;
planePos.y = ceil(rayPos.y / _DistanceBetweenFloors);
planePos.y -= lerp(1.0, 0.0, which);
planePos.y *= _DistanceBetweenFloors;
...
}
// 左右の壁
{
...
planePos.x = ceil(rayPos.x / _DistanceBetweenWalls);
planePos.x -= lerp(1.0, 0.0, which);
planePos.x *= _DistanceBetweenWalls;
...
}
// 奥の壁
{
...
planePos.z = ceil(rayPos.z / _DistanceBetweenWalls);
planePos.z -= lerp(1.0, 0.0, which);
planePos.z *= _DistanceBetweenWalls;
...
}
}
これでいい感じに調整しやすくなりました。
テクスチャを貼る
この平面にテクスチャを貼っていきます。
ひとまずはテクスチャはUVの場所が分かりやすい確認用を使用すると良いかと思います。googleで「uv check texture」で検索すると数値+アルファベットが書かれたテクスチャが出てくるので、その数値を見ながら適切に貼れているか確認しながら作業します。
UVは線と平面の交点から算出していきます。
交点は先程ちらっと出た「L0 + L * t = P」です。
// 床と天井 { ... if (i < intersect) { intersect = i; float3 pos = rayPos + rayDir * i + 0.5; float3 uvw = pos.xzy; color = tex2D(_MainTex, uvw.xy); } ... } // 左右の壁 { ... float3 pos = rayPos + rayDir * i + 0.5; float3 uvw = pos.zyx; color = tex2D(_MainTex, uvw.xy); ... } // 奥の壁 { ... float3 pos = rayPos + rayDir * i + 0.5; float3 uvw = pos.xyz; color = tex2D(_MainTex, uvw.xy); ... }
uvw.xyが平面のUVになります。
Boxの左手前の座標が(-0.5,-0.5)であるため、最後に+0.5を加算し調整します。あとは通常通りtex2D関数を用いて_MainTexから色を取ってくることで、テクスチャを貼ることができます。
しかしよく見ると反転して貼られている箇所があるので、各面に調整が必要です。
この辺りはただただ面倒なだけなので、Tiling&Offsetも含めた最終調整処理がこちらになります。
Properties
{
_FloorTexSizeAndOffset ("Floor Texture Size And Offset", Vector) = (0.5, 0.5, 0.0, 0.0)
_CeilTexSizeAndOffset ("Ceil Texture Size And Offset", Vector) = (0.5, 0.5, 0.0, 0.5)
_WallTexSizeAndOffset ("Wall Texture Size And Offset", Vector) = (0.5, 0.5, 0.5, 0.0)
}
float4 _FloorTexSizeAndOffset;
float4 _CeilTexSizeAndOffset;
float4 _WallTexSizeAndOffset;
//---------------------------------------------------
float2 GetCeilUV(float3 uvw)
{
uvw.x = (uvw.x - 1.0) * _CeilTexSizeAndOffset.x - _CeilTexSizeAndOffset.z;
uvw.y = (uvw.y) * _CeilTexSizeAndOffset.y - _CeilTexSizeAndOffset.w;
return float2(-uvw.x, uvw.y);
}
float2 GetFloorUV(float3 uvw)
{
uvw.x = (uvw.x) * _FloorTexSizeAndOffset.x + _FloorTexSizeAndOffset.z;
uvw.y = (uvw.y) * _FloorTexSizeAndOffset.y + _FloorTexSizeAndOffset.w;
return uvw.xy;
}
float2 GetLeftWallUV(float3 uvw)
{
uvw.x = (uvw.x) * _WallTexSizeAndOffset.x + _WallTexSizeAndOffset.z;
uvw.y = (uvw.y) * _WallTexSizeAndOffset.y + _WallTexSizeAndOffset.w;
return uvw.xy;
}
float2 GetRightWallUV(float3 uvw)
{
uvw.x = (uvw.x - 1.0) * _WallTexSizeAndOffset.x - _WallTexSizeAndOffset.z;
uvw.y = (uvw.y) * _WallTexSizeAndOffset.y + _WallTexSizeAndOffset.w;
return float2(-uvw.x, uvw.y);
}
float2 GetFrontWallUV(float3 uvw)
{
uvw.x = (uvw.x) * _WallTexSizeAndOffset.x + _WallTexSizeAndOffset.z;
uvw.y = (uvw.y) * _WallTexSizeAndOffset.y + _WallTexSizeAndOffset.w;
return uvw.xy;
}
float2 GetBackWallUV(float3 uvw)
{
uvw.x = (uvw.x - 1.0) * _WallTexSizeAndOffset.x - _WallTexSizeAndOffset.z;
uvw.y = (uvw.y) * _WallTexSizeAndOffset.y + _WallTexSizeAndOffset.w;
return float2(-uvw.x, uvw.y);
}
//---------------------------------------------------
これら関数からテクスチャに沿ったUVを取得できます。
TilingやOffsetは私が用意したテクスチャに合わせて数値を調整しています。
このテクスチャをマテリアルのMain Textureにつけることで、
床/天井/壁の区分に沿ったテクスチャが貼られます。
(左下:床、左上:天井、右下:壁、右上:オブジェ)

絵素材は「建築パース.com様」のものを使用しております。
本記事にて再配布しておりますが、停止する可能性もございます。
ご利用の際はご注意ください。
kenchiku-pers.com
ランダム
すいません。力尽きました…orz
実装も雑なので~その2~にて改めます。
//--------------------------------------------------- float rand(float3 co) { return frac(sin(dot(co.xyz, float3(12.9898, 78.233, 56.787))) * 43758.5453); } float3 GetRandomTiledUV(float3 uvw, float between, float tile) { float r = rand(floor((uvw + 0.00001) / between)); // 微妙に内側に入れることでZファイティングを防ぐ r = floor(r * 10000) % tile; uvw.xy = frac(uvw.xy / between); uvw.x += floor(r / (tile / 2)); uvw.y += floor(r % (tile / 2)); uvw.xy = uvw.xy / (tile / 2); uvw.z = r; return uvw; } //--------------------------------------------------- float2 GetCeilUV(float3 uvw) { // これを各GetHogeUVの先頭で処理する uvw = GetRandomTiledUV(uvw, _DistanceBetweenWalls, _Tiles); ...
オブジェクトを置く
人とか犬とか観葉植物を置いたらどんな感じになるの?と思い実装してみました。
参考サイトにもあるように、やっぱり書割感強かったです。
実装は壁と同じように平面にテクスチャを貼ります。
ただし、距離更新を行うまえに透過色かどうかをチェックし、透明だったらスルーするという処理を施します。
// 奥のオブジェクト(人/観葉植物等) { float which = step(0.0, dot(rayDir, FrontVec)); planeNormal = float3(0, 0, lerp(1, -1, which)); planePos.xy = 0.0; planePos.z = ceil(rayPos.z / _DistanceBetweenObject); planePos.z -= lerp(1.0, 0.0, which); planePos.z *= _DistanceBetweenObject; float i = GetIntersectLength(rayPos, rayDir, planePos, planeNormal); if (i < intersect) { float3 pos = rayPos + rayDir * i + 0.5; float3 uvw = pos.xyz; float4 c = lerp(GetBackObjectColor(uvw), GetFrontObjectColor(uvw), which); if(0.5 < c.a) { intersect = i; color = c; } } }

ただし、真横から見た時に薄っぺらい板なのがはっきりしてしまうため、
スパイダーマンのようにシェイプ(Box)の平面毎に内装を変えないとマズいようです。
一見バグのように見えたのですが、そういった都合があるみたいですねぇ。
こちらも余力があれば~その2~に対策処理を施したい…です。
おまけ(視差マップ)
視差マップ(Parallax Mapping)も視線を元に凹凸を表現する技術なので、
相性がよさそうだなぁと思って実装してみました。
ただ結論としてはちょっとビミョイ(調整が足りないせいも多分あります)

おまけ(視差遮蔽マップ)
視差遮蔽マップ(Parallax Occulusion Mapping)も視線とハイトマップを元に凸凹を表現する技術なので、
相性がよさそうだなぁと思って実装してみました。
実装してから結構日が経つのであんまり覚えてないですが、重かったみたいです。
前記事で勉強したParallaxOcclutionMappingとInteriorMappingを融合させてみました。(クソ重くて使い物にならない)#interiormapping #unity3d pic.twitter.com/nsUJ9jBS4b
— コポ🌻本販売 (@coposuke) 2019年1月25日
まとめ
インテリアマップ面白いですよね~。
まだまだ色々なことが出来そうだな~と思うような技術でした!
インテリア以外の用途もヒラメキそうで何も思いつかない!
別の手法
参考資料
http://interiormapping.oogst3d.net/
https://www.habrador.com/tutorials/shaders/2-interior-mapping/
http://www.scratchapixel.com/lessons/3d-basic-rendering/minimal-ray-tracer-rendering-simple-shapes/ray-plane-and-ray-disk-intersection
明日
明日は真史 上山さん(@masakam1)の「unityでのatlas texture2018最新状況」です!